In an ensemble (connected collection) of unsynchronized oscillators, the average energy is spread equally between kinetic and potential types.
In a solid, thermal energy (often referred to loosely as heat content) can be accurately described by an ensemble of thermal phonons that act as mechanical oscillators. In this model, thermal energy is equally kinetic and potential.
In an ideal gas, the interaction potential between particles is essentially the delta function which stores no energy: thus, all of the thermal energy is kinetic.
Because an electric oscillator (LC circuit) is analogous to a mechanical oscillator, its energy must be, on average, equally kinetic and potential. It is entirely arbitrary whether the magnetic energy is considered kinetic and whether the electric energy is considered potential, or vice versa. That is, either the inductor is analogous to the mass while the capacitor is analogous to the spring, or vice versa.
1. By extension of the previous line of thought, in free space the electromagnetic field can be considered an ensemble of oscillators, meaning that radiation energy can be considered equally potential and kinetic. This model is useful, for example, when the electromagnetic Lagrangian is of primary interest and is interpreted in terms of potential and kinetic energy.
2. On the other hand, in the key equation m2c4 = E2 − p2c2, the contribution mc2 is called the rest energy, and all other contributions to the energy are called kinetic energy. For a particle that has mass, this implies that the kinetic energy is 0.5p2 / m at speeds much smaller than c, as can be proved by writing E = mc2 √(1 + p2m − 2c − 2) and expanding the square root to lowest order. By this line of reasoning, the energy of a photon is entirely kinetic, because the photon is massless and has no rest energy. This expression is useful, for example, when the energy-versus-momentum relationship is of primary interest.
The two analyses are entirely consistent. The electric and magnetic degrees of freedom in item 1 are transverse to the direction of motion, while the speed in item 2 is along the direction of motion. For non-relativistic particles these two notions of potential versus kinetic energy are numerically equal, so the ambiguity is harmless, but not so for relativistic particles.
Work and virtual work
Work is force times distance.
This says that the work (W) is equal to the line integral of the force F along a path C; for details see the mechanical work article.
Work and thus energy is frame dependent. For example, consider a ball being hit by a bat. In the center-of-mass reference frame, the bat does no work on the ball. But, in the reference frame of the person swinging the bat, considerable work is done on the ball.
Quantum mechanics
In quantum mechanics energy is defined in terms of the energy operator as a time derivative of the wave function. The Schrödinger equation equates the energy operator to the full energy of a particle or a system. It thus can be considered as a definition of measurement of energy in quantum mechanics. The Schrödinger equation describes the space- and time-dependence of slow changing (non-relativistic) wave function of quantum systems. The solution of this equation for bound system is discrete (a set of permitted states, each characterized by an energy level) which results in the concept of quanta. In the solution of the Schrödinger equation for any oscillator (vibrator) and for electromagnetic waves in a vacuum, the resulting energy states are related to the frequency by the Planck equation E = hν (where h is the Planck's constant and ν the frequency). In the case of electromagnetic wave these energy states are called quanta of light or photons.
Relativity
When calculating kinetic energy (= work to accelerate a mass from zero speed to some finite speed) relativistically - using Lorentz transformations instead of Newtonian mechanics, Einstein discovered an unexpected by-product of these calculations to be an energy term which does not vanish at zero speed. He called it rest mass energy - energy which every mass must possess even when being at rest. The amount of energy is directly proportional to the mass of body:
- E = mc2,
where
- m is the mass,
- c is the speed of light in vacuum,
- E is the rest mass energy.
For example, consider electron-positron annihilation, in which the rest mass of individual particles is destroyed, but the inertia equivalent of the system of the two particles (its invariant mass) remains (since all energy is associated with mass), and this inertia and invariant mass is carried off by photons which individually are massless, but as a system retain their mass. This is a reversible process - the inverse process is called pair creation - in which the rest mass of particles is created from energy of two (or more) annihilating photons.
In general relativity, the stress-energy tensor serves as the source term for the gravitational field, in rough analogy to the way mass serves as the source term in the non-relativistic Newtonian approximation.[14]
It is not uncommon to hear that energy is "equivalent" to mass. It would be more accurate to state that every energy has inertia and gravity equivalent, and because mass is a form of energy, then mass too has inertia and gravity associated with it.
Measurement
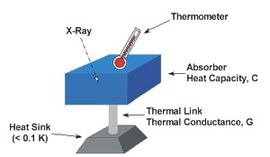
There is no absolute measure of energy, because energy is defined as the work that one system does (or can do) on another. Thus, only the transition of a system from one state into another can be defined and thus measured.
Methods
The methods for the measurement of energy often deploy methods for the measurement of still more fundamental concepts of science, namely mass, distance, radiation, temperature, time, electric charge and electric current.
Conventionally the technique most often employed is calorimetry, a thermodynamic technique that relies on the measurement of temperature using a thermometer or of intensity of radiation using a bolometer.

No comments:
Post a Comment