
Classical mechanics distinguishes between potential energy, which is a function of the position of an object, and kinetic energy, which is a function of its movement. Both position and movement are relative to a frame of reference, which must be specified: this is often (and originally) an arbitrary fixed point on the surface of the Earth, the terrestrial frame of reference. It has been attempted to categorize all forms of energy as either kinetic or potential: this is not incorrect, but neither is it clear that it is a real simplification, as Feynman points out:
These notions of potential and kinetic energy depend on a notion of length scale. For example, one can speak of macroscopic potential and kinetic energy, which do not include thermal potential and kinetic energy. Also what is called chemical potential energy (below) is a macroscopic notion, and closer examination shows that it is really the sum of the potential and kinetic energy on the atomic and subatomic scale. Similar remarks apply to nuclear "potential" energy and most other forms of energy. This dependence on length scale is non-problematic if the various length scales are decoupled, as is often the case ... but confusion can arise when different length scales are coupled, for instance when friction converts macroscopic work into microscopic thermal energy.
| Mechanical energy is converted | |
|---|---|
| into | by |
| Mechanical energy | Lever |
| Thermal energy | Brakes |
| Electric energy | Dynamo |
| Electromagnetic radiation | Synchrotron |
| Chemical energy | Matches |
| Nuclear energy | Particle accelerator |
Mechanical energy
Mechanical energy manifest in many forms,but can be broadly classified into elastic potential energy and kinetic energy. The term potential energy is a very general term, because it exists in all force fields, such as gravitation, electrostatic and magnetic fields. Potential energy refers to the energy any object gets due to its position in a force field.
Potential energy, symbols Ep, V or Φ, is defined as the work done against a given force (= work of given force with minus sign) in changing the position of an object with respect to a reference position (often taken to be infinite separation). If F is the force and s is the displacement,
with the dot representing the scalar product of the two vectors.
The name "potential" energy originally signified the idea that the energy could readily be transferred as work—at least in an idealized system (reversible process, see below). This is not completely true for any real system, but is often a reasonable first approximation in classical mechanics.
The general equation above can be simplified in a number of common cases, notably when dealing with gravity or with elastic forces.
Elastic potential energy

Elastic potential energy is defined as a work needed to compress (or expand) a spring. The force, F, in a spring or any other system which obeys Hooke's law is proportional to the extension or compression, x,
-
- F = − kx
where k is the force constant of the particular spring (or system). In this case, the calculated work becomes
only when k is constant. Hooke's law is a good approximation for behaviour of chemical bonds under normal conditions, i.e. when they are not being broken or formed.
Kinetic energy
Kinetic energy, symbols Ek, T or K, is the work required to accelerate an object to a given speed. Indeed, calculating this work one easily obtains the following:
At speeds approaching the speed of light, c, this work must be calculated using Lorentz transformations, which results in the following:
This equation reduces to the one above it, at small (compared to c) speed. A mathematical by-product of this work (which is immediately seen in the last equation) is that even at rest a mass has the amount of energy equal to:
-
- Erest = mc2
This energy is thus called rest mass energy.
Surface energy
If there is any kind of tension in a surface, such as a stretched sheet of rubber or material interfaces, it is possible to define surface energy. In particular, any meeting of dissimilar materials that don't mix will result in some kind of surface tension, if there is freedom for the surfaces to move then, as seen in capillary surfaces for example, the minimum energy will as usual be sought.
A minimal surface, for example, represents the smallest possible energy that a surface can have if its energy is proportional to the area of the surface. For this reason, (open) soap films of small size are minimal surfaces (small size reduces gravity effects, and openness prevents pressure from building up. Note that a bubble is a minimum energy surface but not a minimal surface by definition).
Sound energy
Sound is a form of mechanical vibration, which propagates through any mechanical medium.
Gravitational energy
The gravitational force near the Earth's surface varies very little with the height, h, and is equal to the mass, m, multiplied by the gravitational acceleration, g = 9.81 m/s². In these cases, the gravitational potential energy is given by
-
- Ep,g = mgh
A more general expression for the potential energy due to Newtonian gravitation between two bodies of masses m1 and m2, useful in astronomy, is
-
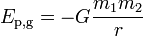 ,
,
where r is the separation between the two bodies and G is the gravitational constant, 6.6742(10)×10−11 m3kg−1s−2.[19] In this case, the reference point is the infinite separation of the two bodies.
Thermal energy
| Thermal energy is converted | |
|---|---|
| into | by |
| Mechanical energy | Steam turbine |
| Thermal energy | Heat exchanger |
| Electric energy | Thermocouple |
| Electromagnetic radiation | Hot objects |
| Chemical energy | Blast furnace |
| Nuclear energy | Supernova |
Thermal energy (of some media - gas, plasma, solid, etc) is the energy associated with the microscopical random motion of particles constituting the media. For example, in case of monoatomic gas it is just a kinetic energy of motion of atoms of gas as measured in the reference frame of the center of mass of gas. In case of many-atomic gas rotational and vibrational energy is involved. In the case of liquids and solids there is also potential energy (of interaction of atoms) involved, and so on.
A heat is defined as a transfer (flow) of thermal energy across certain boundary (for example, from a hot body to cold via the area of their contact. A practical definition for small transfers of heat is
where Cv is the heat capacity of the system. This definition will fail if the system undergoes a phase transition—e.g. if ice is melting to water—as in these cases the system can absorb heat without increasing its temperature. In more complex systems, it is preferable to use the concept of internal energy rather than that of thermal energy (see Chemical energy below).
Despite the theoretical problems, the above definition is useful in the experimental measurement of energy changes. In a wide variety of situations, it is possible to use the energy released by a system to raise the temperature of another object, e.g. a bath of water. It is also possible to measure the amount of electric energy required to raise the temperature of the object by the same amount. The calorie was originally defined as the amount of energy required to raise the temperature of one gram of water by 1 °C (approximately 4.1855 J, although the definition later changed), and the British thermal unit was defined as the energy required to heat one pound of water by 1 °F (later fixed as 1055.06 J).
Electric energy
| Electric energy is converted | |
|---|---|
| into | by |
| Mechanical energy | Electric motor |
| Thermal energy | Resistor |
| Electric energy | Transformer |
| Electromagnetic radiation | Light-emitting diode |
| Chemical energy | Electrolysis |
| Nuclear energy | Synchrotron |
Electrostatic energy
The electric potential energy of given configuration of charges is defined as the work which must be done against the Coulomb force to rearrange charges from infinite separation to this configuration (or the work done by the Coulomb force separating the charges from this configuration to infinity). For two point-like charges Q1 and Q2 at a distance r this work, and hence electric potential energy is equal to:
where ε0 is the electric constant of a vacuum, 107/4πc0² or 8.854188…×10−12 F/m.[19] If the charge is accumulated in a capacitor (of capacitance C), the reference configuration is usually selected not to be infinite separation of charges, but vice versa - charges at an extremely close proximity to each other (so there is zero net charge on each plate of a capacitor). The justification for this choice is purely practical - it is easier to measure both voltage difference and magnitude of charges on a capacitor plates not versus infinite separation of charges but rather versus discharged capacitor where charges return to close proximity to each other (electrons and ions recombine making the plates neutral). In this case the work and thus the electric potential energy becomes
Electricity energy
If an electric current passes through a resistor, electric energy is converted to heat; if the current passes through an electric appliance, some of the electric energy will be converted into other forms of energy (although some will always be lost as heat). The amount of electric energy due to an electric current can be expressed in a number of different ways:
where U is the electric potential difference (in volts), Q is the charge (in coulombs), I is the current (in amperes), t is the time for which the current flows (in seconds), P is the power (in watts) and R is the electric resistance (in ohms). The last of these expressions is important in the practical measurement of energy, as potential difference, resistance and time can all be measured with considerable accuracy.
Magnetic energy
There is no fundamental difference between magnetic energy and electric energy: the two phenomena are related by Maxwell's equations. The potential energy of a magnet of magnetic moment m in a magnetic field B is defined as the work of magnetic force (actually of magnetic torque) on re-alignment of the vector of the magnetic dipole moment, and is equal:
while the energy stored in a inductor (of inductance L) when current I is passing via it is
-
 .
.
This second expression forms the basis for superconducting magnetic energy storage.
Electromagnetic Energy
| Electromagnetic radiation is converted | |
|---|---|
| into | by |
| Mechanical energy | Solar sail |
| Thermal energy | Solar collector |
| Electric energy | Solar cell |
| Electromagnetic radiation | Non-linear optics |
| Chemical energy | Photosynthesis |
| Nuclear energy | Mössbauer spectroscopy |
Calculating work needed to create an electric or magnetic field in unit volume (say, in a capacitor or an inductor) results in the electric and magnetic fields energy densities:
and
-
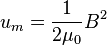 ,
,
in SI units.
Electromagnetic radiation, such as microwaves, visible light or gamma rays, represents a flow of electromagnetic energy. Applying the above expressions to magnetic and electric components of electromagnetic field both the volumetric density and the flow of energy in e/m field can be calculated. The resulting Poynting vector, which is expressed as
in SI units, gives the density of the flow of energy and its direction.
The energy of electromagnetic radiation is quantized (has discrete energy levels). The spacing between these levels is equal to
-
- E = hν
where h is the Planck constant, 6.6260693(11)×10−34 Js,[19] and ν is the frequency of the radiation. This quantity of electromagnetic energy is usually called a photon. The photons which make up visible light have energies of 270–520 yJ, equivalent to 160–310 kJ/mol, the strength of weaker chemical bonds.
Chemical energy
| Chemical energy is converted | |
|---|---|
| into | by |
| Mechanical energy | Muscle |
| Thermal energy | Fire |
| Electric energy | Fuel cell |
| Electromagnetic radiation | Glowworms |
| Chemical energy | Chemical reaction |
Chemical energy is the energy due to associations of atoms in molecules and various other kinds of aggregates of matter. It may be defined as a work done by electric forces during re-arrangement of mutual positions of electric charges, electrons and protons, in the process of aggregation. So, basically it is electrostatic potential energy of electric charges. If the chemical energy of a system decreases during a chemical reaction, the difference is transferred to the surroundings in some form (often heat or light); on the other hand if the chemical energy of a system increases as a result of a chemical reaction - the difference then is supplied by the surroundings (usually again in form of heat or light). For example,
- when two hydrogen atoms react to form a dihydrogen molecule, the chemical energy decreases by 724 zJ (the bond energy of the H–H bond);
- when the electron is completely removed from a hydrogen atom, forming a hydrogen ion (in the gas phase), the chemical energy increases by 2.18 aJ (the ionization energy of hydrogen).
It is common to quote the changes in chemical energy for one mole of the substance in question: typical values for the change in molar chemical energy during a chemical reaction range from tens to hundreds of kilojoules per mole.
The chemical energy as defined above is also referred to by chemists as the internal energy, U: technically, this is measured by keeping the volume of the system constant. Most practical chemistry is performed at constant pressure and, if the volume changes during the reaction (e.g. a gas is given off), a correction must be applied to take account of the work done by or on the atmosphere to obtain the enthalpy, H:
-
- ΔH = ΔU + pΔV
A second correction, for the change in entropy, S, must also be performed to determine whether a chemical reaction will take place or not, giving the Gibbs free energy, G:
-
- ΔG = ΔH − TΔS
These corrections are sometimes negligible, but often not (especially in reactions involving gases).
Since the industrial revolution, the burning of coal, oil, natural gas or products derived from them has been a socially significant transformation of chemical energy into other forms of energy. the energy "consumption" (one should really speak of "energy transformation") of a society or country is often quoted in reference to the average energy released by the combustion of these fossil fuels:
- 1 tonne of coal equivalent (TCE) = 29.3076 GJ = 8,141 kilowatt hour
- 1 tonne of oil equivalent (TOE) = 41.868 GJ = 11,630 kilowatt hour
On the same basis, a tank-full of gasoline (45 litres, 12 gallons) is equivalent to about 1.6 GJ of chemical energy. Another chemically-based unit of measurement for energy is the "tonne of TNT", taken as 4.184 GJ. Hence, burning a tonne of oil releases about ten times as much energy as the explosion of one tonne of TNT: fortunately, the energy is usually released in a slower, more controlled manner.
Simple examples of storage of chemical energy are batteries and food. When food is digested and metabolized (often with oxygen), chemical energy is released, which can in turn be transformed into heat, or by muscles into kinetic energy.
Nuclear energy
| Nuclear binding energy is converted | |
|---|---|
| into | by |
| Mechanical energy | Alpha radiation |
| Thermal energy | Sun |
| Electrical energy | Beta radiation |
| Electromagnetic radiation | Gamma radiation |
| Chemical energy | Radioactive decay |
| Nuclear energy | Nuclear isomerism |
Nuclear potential energy, along with electric potential energy, provides the energy released from nuclear fission and nuclear fusion processes. The result of both these processes are nuclei in which the more-optimal size of the nucleus allows the nuclear force (which is opposed by the electromagnetic force) to bind nuclear particles more tightly together than before the reaction.
The Weak nuclear force (different from the strong force) provides the potential energy for certain kinds of radioactive decay, such as beta decay.
The energy released in nuclear processes is so large that the relativistic change in mass (after the energy has been removed) can be as much as several parts per thousand.
Nuclear particles (nucleons) like protons and neutrons are not destroyed (law of conservation of baryon number) in fission and fusion processes. A few lighter particles may be created or destroyed (example: beta minus and beta plus decay, or electron capture decay), but these minor processes are not important to the immediate energy release in fission and fusion. Rather, fission and fusion release energy when collections of baryons become more tightly bound, and it is the energy associated with a fraction of the mass of the nucleons (but not the whole particles) which appears as the heat and electromagnetic radiation generated by nuclear reactions. This heat and radiation retains the "missing" mass, but the mass is missing only because it escapes in the form of heat and light, which retain the mass and conduct it out of the system where it is not measured.
The energy from the Sun, also called solar energy, is an example of this form of energy conversion. In the Sun, the process of hydrogen fusion converts about 4 million metric tons of solar matter per second into light, which is radiated into space, but during this process, the number of total protons and neutrons in the sun does not change. In this system, the light itself retains the inertial equivalent of this mass, and indeed the mass itself (as a system), which represents 4 million tons per second of electromagnetic radiation, moving into space. Each of the helium nuclei which are formed in the process are less massive than the four protons from they were formed, but (to a good approximation), no particles or atoms are destroyed in the process of turning the sun's nuclear potential energy into light.
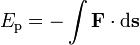

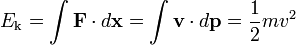


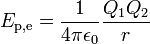

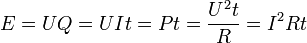

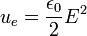

No comments:
Post a Comment