Energy is subject to a strict global conservation law; that is, whenever one measures (or calculates) the total energy of a system of particles whose interactions do not depend explicitly on time, it is found that the total energy of the system always remains constant.[12]
- The total energy of a system can be subdivided and classified in various ways. For example, it is sometimes convenient to distinguish potential energy (which is a function of coordinates only) from kinetic energy (which is a function of coordinate time derivatives only). It may also be convenient to distinguish gravitational energy, electric energy, thermal energy, and other forms. These classifications overlap; for instance, thermal energy usually consists partly of kinetic and partly of potential energy.
- The transfer of energy can take various forms; familiar examples include work, heat flow, and advection, as discussed below.
- The word "energy" is also used outside of physics in many ways, which can lead to ambiguity and inconsistency. The vernacular terminology is not consistent with technical terminology. For example, while energy is always conserved (in the sense that the total energy does not change despite energy transformations), energy can be converted into a form, e.g., thermal energy, that cannot be utilized to perform work. When one talks about "conserving energy by driving less," one talks about conserving fossil fuels and preventing useful energy from being lost as heat. This usage of "conserve" differs from that of the law of conservation of energy.[13]
In classical physics energy is considered a scalar quantity, the canonical conjugate to time. In special relativity energy is also a scalar (although not a Lorentz scalar but a time component of the energy-momentum 4-vector).[14] In other words, energy is invariant with respect to rotations of space, but not invariant with respect to rotations of space-time (= boosts).
Energy transfer
Because energy is strictly conserved and is also locally conserved (wherever it can be defined), it is important to remember that by the definition of energy the transfer of energy between the "system" and adjacent regions is work. A familiar example is mechanical work. In simple cases this is written as the following equation:
- ΔE = W (1)
if there are no other energy-transfer processes involved. Here E is the amount of energy transferred, and W represents the work done on the system.
More generally, the energy transfer can be split into two categories:
- ΔE = W + Q (2)
where Q represents the heat flow into the system.
There are other ways in which an open system can gain or lose energy. In chemical systems, energy can be added to a system by means of adding substances with different chemical potentials, which potentials are then extracted (both of these process are illustrated by fueling an auto, a system which gains in energy thereby, without addition of either work or heat). Winding a clock would be adding energy to a mechanical system. These terms may be added to the above equation, or they can generally be subsumed into a quantity called "energy addition term E" which refers to any type of energy carried over the surface of a control volume or system volume. Examples may be seen above, and many others can be imagined (for example, the kinetic energy of a stream of particles entering a system, or energy from a laser beam adds to system energy, without either being either work-done or heat-added, in the classic senses).
- ΔE = W + Q + E (3)
Where E in this general equation represents other additional advected energy terms not covered by work done on a system, or heat added to it.
Energy is also transferred from potential energy (Ep) to kinetic energy (Ek) and then back to potential energy constantly. This is referred to as conservation of energy. In this closed system, energy cannot be created or destroyed; therefore, the initial energy and the final energy will be equal to each other. This can be demonstrated by the following:
- Epi + Eki = EpF + EkF
The equation can then be simplified further since Ep = mgh (mass times acceleration due to gravity times the height) and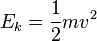 
(half mass times velocity squared). Then the total amount of energy can be found by adding Ep + Ek = Etotal.
Energy and the laws of motion
| Classical mechanics | ||||||
 Newton's Second Law | ||||||
History of ...
| ||||||
In classical mechanics, energy is a conceptually and mathematically useful property, as it is a conserved quantity.
The Hamiltonian
The total energy of a system is sometimes called the Hamiltonian, after William Rowan Hamilton. The classical equations of motion can be written in terms of the Hamiltonian, even for highly complex or abstract systems. These classical equations have remarkably direct analogs in nonrelativistic quantum mechanics.[15]
The Lagrangian
Another energy-related concept is called the Lagrangian, after Joseph Louis Lagrange. This is even more fundamental than the Hamiltonian, and can be used to derive the equations of motion. It was invented in the context of classical mechanics, but is generally useful in modern physics. The Lagrangian is defined as the kinetic energy minus the potential energy.
Usually, the Lagrange formalism is mathematically more convenient than the Hamiltonian for non-conservative systems (such as systems with friction).
Energy and thermodynamics
Internal energy
Internal energy is the sum of all microscopic forms of energy of a system. It is related to the molecular structure and the degree of molecular activity and may be viewed as the sum of kinetic and potential energies of the molecules; it comprises the following types of energy:[16]
| Type | Composition of internal energy (U) |
|---|---|
| Sensible energy | the portion of the internal energy of a system associated with kinetic energies (molecular translation, rotation, and vibration; electron translation and spin; and nuclear spin) of the molecules. |
| Latent energy | the internal energy associated with the phase of a system. |
| Chemical energy | the internal energy associated with the different kinds of aggregation of atoms in matter. |
| Nuclear energy | the tremendous amount of energy associated with the strong bonds within the nucleus of the atom itself. |
| Energy interactions | those types of energies that are not stored in the system (e.g. heat transfer, mass transfer, and work), but are recognized at the system boundary as they cross it, representing gains or losses by a system during a process. |
| Thermal energy | the sum of sensible and latent forms of internal energy. |
The laws of thermodynamics
According to the second law of thermodynamics, work can be totally converted into heat, but not vice versa. This is a mathematical consequence of statistical mechanics. The first law of thermodynamics simply asserts that energy is conserved,[17] and that heat is included as a form of energy transfer. A commonly-used corollary of the first law is that for a "system" subject only to pressure forces and heat transfer (e.g., a cylinder-full of gas), the differential change in energy of the system (with a gain in energy signified by a positive quantity) is given as the following equation:
,
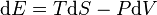where the first term on the right is the heat transfer into the system, defined in terms of temperature T and entropy S (in which entropy increases and the change dS is positive when the system is heated), and the last term on the right hand side is identified as "work" done on the system, where pressure is P and volume V (the negative sign results since compression of the system requires work to be done on it and so the volume change, dV, is negative when work is done on the system). Although this equation is the standard textbook example of energy conservation in classical thermodynamics, it is highly specific, ignoring all chemical, electric, nuclear, and gravitational forces, effects such as advection of any form of energy other than heat, and because it contains a term that depends on temperature. The most general statement of the first law (i.e., conservation of energy) is valid even in situations in which temperature is undefinable.
Energy is sometimes expressed as the following equation:
,
which is unsatisfactory[13] because there cannot exist any thermodynamic state functions W or Q that are meaningful on the right hand side of this equation, except perhaps in trivial cases.
Equipartition of energy
The energy of a mechanical harmonic oscillator (a mass on a spring) is alternatively kinetic and potential. At two points in the oscillation cycle it is entirely kinetic, and alternatively at two other points it is entirely potential. Over the whole cycle, or over many cycles, net energy is thus equally split between kinetic and potential. This is called equipartition principle; total energy of a system with many degrees of freedom is equally split among all available degrees of freedom.
This principle is vitally important to understanding the behavior of a quantity closely related to energy, called entropy. Entropy is a measure of evenness of a distribution of energy between parts of a system. When an isolated system is given more degrees of freedom (i.e., given new available energy states that are the same as existing states), then total energy spreads over all available degrees equally without distinction between "new" and "old" degrees. This mathematical result is called the second law of thermodynamics.
No comments:
Post a Comment